A look at an automatic circuit analysis program through engineering-based examples.
SCEPTRE is an automatic circuit analysis program capable of determining initial condition, transient, frequency and steady-state response of electrical networks and dynamic systems. It is considered a general-purpose tool for engineers and can be used to assist in the design and analysis of various circuits. The problem of interest is described in a free-format, easy-to-learn, engineer-oriented language. The basic set of network elements consists of linear and nonlinear resistors, capacitors, inductors, voltage and current sources, and mutual inductances.
In addition, SCEPTRE has a “Defined Parameter” mode allowing it to solve state equations, which might be written to describe non-electrical systems. This outstanding feature allows the user to couple electrical networks with differential equation systems giving a great deal of versatility, especially for interdisciplinary problems like mechatronics.
If the problem of interest cannot be described by the built-in functions, the user can describe his problem as an ultima ratio via a FORTRAN program. The program uses the state variable method. Other highlights are the model library, reruns with automatic varied network quantities, extended DC options (sensitivity, worst-case, Monte Carlo, optimization), and several integration routines for accurate and fast solution of even “stiff” problems.
Example Problem
To give the uninitiated some idea of the input data required to accommodate a simple but practical problem, consider the electrical schematic of the Darlington pair in Figure 1. The SCEPTRE version of the circuit appears in Figure 2 with the assumption that a transistor equivalent circuit named 2N706A has been stored in the model library at some previous time.
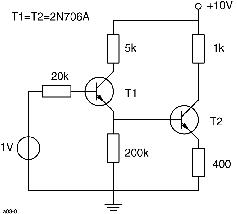
Figure 1. Schematic Diagram of Darlington Pair
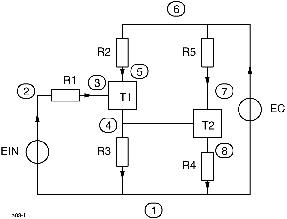
Figure 2. SCEPTRE Form of Darlington Pair
The problem is to determine the output voltages across R3 and R4 and the power requirements of this circuit under nominal conditions and after the current gain of the first-stage transistor has been degraded to various levels. Defined Parameters will be used to calculate the power consumption (PEC, PEIN). The rerun feature accommodates the additional runs required for the degraded alpha version (P1T1). The SCEPTRE input is shown in Listing 1.
Listing 1. SCEPTRE Input
CIRCUIT DESCRIPTION Darlington pair ELEMENTS EC , 1-6 = 10 EIN , 1-2 = 1 R1 , 2-3 = 20 R2 , 6-5 = 5 R3 , 4-1 = 200 R4 , 8-1 = .4 R5 , 6-7 = 1 T1 , 3-4-5 = MODEL 2N706A (PERM) T2 , 4-8-7 = MODEL 2N706A (PERM) DEFINED PARAMETERS PEC = X1 (EC*IEC) PEIN= X2 (EIN*IEIN) OUTPUTS PEC,PEIN,VR3,VR4 RUN CONTROLS RUN INITIAL CONDITIONS ONLY RERUN DESCRIPTION (3) DEFINED PARAMETERS P1T1= .96, .93, .9 END
SCEPTRE Use
This section describes the preparation of circuits and the basics of the circuit description language for better understanding of the examples.
Circuit Preparation
Assuming the user wants to analyse an electric circuit, the following steps should be considered:
- Draw an equivalent circuit consisting of resistors, capacitors, inductors, mutual inductances, voltage sources, current sources or models containing these elements. All of these elements may be linear or nonlinear.
- Assign to each node an arbitrary alphanumeric name.
- Give each element in the circuit a unique name, where the first character classifies the component according to Table 1.
Table 1. Character-Component Relationship
| Character | Element |
| R | resistor |
| C | capacitor |
| L | inductor |
| M | mutual inductance |
| E | voltage source |
| J | current source |
- Choose a consistent set of parameter units. SCEPTRE assumes no set of units for the element values. It operates directly on the numbers supplied by the user. For numerical reasons, users should select a set of units so that the voltage and current responses expected in the solution are as close to unity as possible. A consistent set of units is one which satisfies the following equations simultaneously: U = I R, t = R C = L/R.
- Choose an arbitrary current flow in each passive circuit element, indicate the direction of positive current flow in each current source and voltage source.
SCEPTRE statements are entered under major headings and subheadings. The most important headings used are the following:
MODEL DESCRIPTION CIRCUIT DESCRIPTION ELEMENTS DEFINED PARAMETERS OUTPUTS FUNCTIONS RERUN DESCRIPTION END
The actual problem is described under the major heading CIRCUIT DESCRIPTION. For the temporary definition or permanent storage of models, the corresponding input data go under the heading MODEL DESCRIPTION. The RERUN DESCRIPTION heading is always used whenever the rerun feature is exercised. All changes to the master network must appear under this heading.
The network topology of a circuit must be written under the subheading ELEMENTS in the general form:
element, fromnode - tonode = value
in case of mutual inductances:
M..., Lname1 - Lname2 = value
value may be a number, defined parameter, reference to a table, mathematical expression using any intrinsic FORTRAN function, reference to a statement function or user-defined FORTRAN function.
Controlled sources (E…, J…) may depend on any circuit quantity (linearly dependent sources). Mainly for the analysis of semiconductor devices, current sources may depend on diode tables or built-in diode equations (primary dependent current sources) or even on other primary dependent current sources (secondary dependent current sources). In this way, the simulation is carried out in a cost-effective manner. SCEPTRE determines the correct sequence for the circuit calculation to avoid computational delays normally introduced by these nonlinearities. The controlled sources will run in an AC analysis without modification.
For the Monte Carlo, worst-case and optimization calculations, resistors and sources may be provided by bounds.
Mathematical expressions are entered in two ways. The direct way has the general form
X name (mathematical_definition)
and is preferred when handling an equation, which is used only by a single reference. Using the mathematical sequence for several purposes, the equation form
Q name (par1, par2, ... ) = ( ... )
is the more efficient way. It serves as a statement function and must be entered under the subheading FUNCTIONS.
The same subheading holds the table entries. Data are entered as point pairs with the independent variable in increasing algebraic order. To produce step functions, it is permissible to supply two consecutive independent-variable values that are equal but have different dependent-variable values.
Reference to an element voltage and element current is accomplished by prefixing the element name with the single character V and I, respectively. These references may be used as output variables under the subheading OUTPUTS, expressions, equations, tables and defined parameters. One of the most powerful features in SCEPTRE is the user-defined parameters under the subheading DEFINED PARAMETERS. The general form is
P name = value
where value denotes the possible entries mentioned before. If the user specifies the time derivative
DP name = value
SCEPTRE calculates the integral:
P name = ò DP name dt
This allows the solution of simultaneous differential equations, which need not be coupled to any network quantity. By canonical substitution, transfer functions to any order can be evaluated. Thus, the subheading ELEMENTS is not mandatory. For the AC analysis, the defined parameters may be complex-valued.
A variety of run controls can be entered under the subheading RUN CONTROLS and used to control the simulation to a fine degree.
Simulation
The simulation is carried out in two phases. In the first phase, SCEPTRE analyses the input data and, if the input statements are free of errors, generates the appropriate FORTRAN subroutines which solve the network equations. In the second phase, these subroutines are compiled and linked with modules from the SCEPTRE library and eventually with user-defined routines. Finally, the binary to be executed contains only those modules needed by the actual problem. Moreover, the working buffers are dimensioned accordingly.
During execution, the actual simulation time (or frequency in the AC analysis) with the requested output quantities is monitored (no graphics), but may be suppressed to considerably speed up the simulation. The results are written into a direct access file.
A postprocessor called NGP is available, which reads the direct access file and enables the user to select the requested quantities. NGP then calls GNUPLOT for the final graphical representation.
Despite its apparent complexity, to get full use of SCEPTRE, only a text editor is needed along with two system commands to start the simulation and the postprocessing.
Program Organization
It was the intention of the author to keep the organization of SCEPTRE as simple as possible without losing its power. The shell scripts for SCEPTRE and NGP, which control the flow of all actions, are kept simple, allowing the user to modify them according to his requirements. NGP comes with the source code. Thus, it is possible to adapt NGP to graphic software other than GNUPLOT. Moreover, the monitoring interface routine, which is called after each time or frequency step, is also available as source and may be modified for on-line graphics.
Requirements and Availability
The version of SCEPTRE now available runs under any Linux kernel. It needs a FORTRAN compiler and GNUPLOT. The X11 Window System is not required. The binaries of SCEPTRE, including libraries, NGP (source), auxiliary routines (source), English and German documentation and a set of examples are available at ftp://novilux.fh-friedberg.de/pub/sceptre_linux. The archive also contains a suitable GNUPLOT version and a FORTRAN compiler.
History
SCEPTRE was originally developed by IBM Federal Systems Division, Owego, New York, for the Air Force Weapons Laboratory, Kirtland AFB, New Mexico, in 1966 (see Resources 1-5). The development was assumed by GTE Sylvania, Waltham, Mass., in 1972. The program could be obtained from AFWL for certain mainframes.
Examples
Typical applications for the use of SCEPTRE are circuits with semiconductor devices. Equivalent circuits for these devices are available with any desired complexity (see Resources 5-8).
To demonstrate the wide range of SCEPTRE applications, I will present two examples from different areas. Other examples are included with the listings in the file ftp://ftp.linuxjournal.com/pub/lj/listings/issue63/3008.tgz.
1. High Voltage Impulse Generator
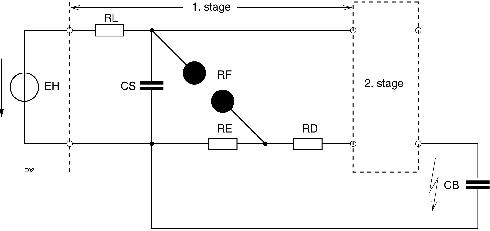
Figure 3. Schematic of a Two-stage Marx-Surge Generator
Voltage pulses of large amplitude are generated when capacitors initially charged in parallel are series-connected with the aid of spark gaps. Such a Marx-surge generator is illustrated in Figure 3. For testing high voltage equipment, e.g., a power transformer, the shape of the generated impulse must meet certain requirements (rise and breakdown time). The shape is influenced mainly by the resistors RE and RD. To save computing time, the capacitors CS in stages 1 and 2 are initially charged via INITIAL CONDITIONS to the voltage of EH (making EH superfluous).
As the stages are identical, the MODEL DESCRIPTION is used and each stage is included with a simple statement in the CIRCUIT DESCRIPTION. To avoid ambiguity of the element names in the main circuit, SCEPTRE includes the model designation as a suffix (here S1 and S2) to the component names. For simplicity, the spark is replaced by a constant resistance RF, but any other nonlinear function may be applied. For this example, the set of units chosen were kV, A, k omega, nF, mH and mus. The voltage at the capacitor CB is referred to as VCB and is shown in Figure 4. The SCEPTRE input is shown in Listing 2.
Listing 2. Marx-Surge Generator Input to SCEPTRE
MODEL DESCRIPTION
MODEL MARX1 (A1-A2-E1-E2)
ELEMENTS
RL, A2-E2 = 300
CS, E2-A1 = 5
RF, E2-AE = 0.001
RE, A1-AE = 12.6
RD, AE-E1 = 0.88
CIRCUIT DESCRIPTION
ELEMENTS
EH, 00-05 = 60
S1, 00-05-10-15 = MODEL MARX1
S2, 10-15-20-25 = MODEL MARX1
CB, 20-00 = .25
INITIAL CONDITIONS
VCSS1 = 60
VCSS2 = 60
OUTPUTS
VCB
RUN CONTROLS
INTEGRATION ROUTINE = IMPLICIT
STOP TIME = 100
END
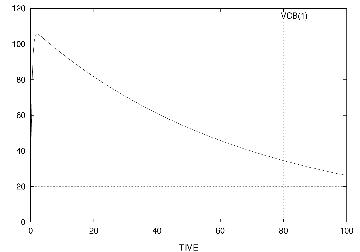
Figure 4. Output Voltage VCB
2. Rotational system

Figure 5. Rotating System with Two Degrees of Freedom, Electrical Analog of System
Figure 5 shows a rotational system with two degrees of freedom. Two bearings with polar moments of inertia J_1 and J_2 and viscous frictions c_1 and c_2 are coupled through a shaft with a spring constant k. A driving torque M is applied to the left bearing. It is desirable to find the angular velocities omega_1 and omega_2 of the bearings and the torque M_w on the shaft.
One approach is to derive directly the mechanical relationship, which yields in the following differential equations (see Resources 3):
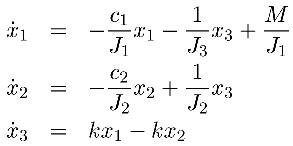
with the substitutions
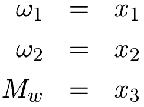
This set of equations can be entered directly under DEFINED PARAMETERS.
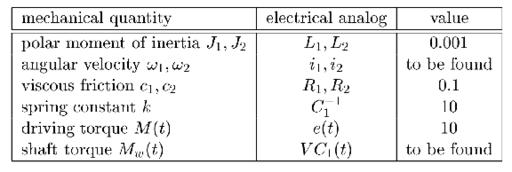
Another method for solving this problem is converting the non-electrical system to its electrical analog as shown in Figure 5. The corresponding mechanical and electrical analogs for this problem are shown in Table 2.
Listing 3. Rotating System Input to SCEPTRE
CIRCUIT DESCRIPTION DEFINED PARAMETERS DPX1 = X1 (-100.*PX1-1000.*PX3+1.E4) DPX2 = X2 (-100.*PX2+1000.*PX3) DPX3 = X3 (10.*PX1-10.*PX2) PX1 = 0 PX2 = 0 PX3 = 0 PERAB3 = X13 (PX3-VC1) ELEMENTS E1, 5-1 = 10 C1, 3-5 = 0.1 R1, 2-3 = 0.1 R2, 4-5 = 0.1 L1, 1-2 = 1E-3 L2, 3-4 = 1E-3 OUTPUTS PX1(W1), PX2(W2), PX3(TS), IR1(I1) IR2(I2), VC1(VC), PERAB3 RUN CONTROLS STOP TIME = .099 END
The SCEPTRE input to solve these two methods simultaneously and independently is shown in Listing 3. The defined parameter PERAB3 has been introduced to monitor the absolute error between the equivalent quantities PX3 and VC1. The functions of time for these quantities are shown in Figure 6. The absolute error PERAB3 remains less than 1.5E-15 during the complete simulation.
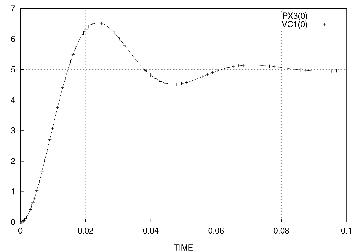
Figure 6. Output Voltage VC1 and Shaft Moment PX3
Conclusion
As can be seen from the examples, SCEPTRE is able to solve problems in a wide range of applications and is not limited to electrical engineering. It produces solutions without requiring the user to do any real programming or write equations. The Defined Parameter mode offers the greatest versatility. Avoiding any programming overhead, the problem to be solved is limited only by the ingenuity and experience of the user.
 Linux, Linux OS, Free Linux Operating System, Linux India Linux, Linux OS,Free Linux Operating System,Linux India supports Linux users in India, Free Software on Linux OS, Linux India helps to growth Linux OS in India
Linux, Linux OS, Free Linux Operating System, Linux India Linux, Linux OS,Free Linux Operating System,Linux India supports Linux users in India, Free Software on Linux OS, Linux India helps to growth Linux OS in India