Part 2 brings us optimization techniques for speeding up code to get the best performance from your Alpha or other RISC processor.
In this article, I will discuss techniques to optimize code for platforms running Linux on Alpha processors. It is based on four years of experience with the Alpha architecture. The primary lesson from this experience is that, for many applications, the memory system, and not the processor itself, is the primary bottleneck. For this reason, most techniques are targeted at avoiding the memory system bottleneck. Since the gap between processor and memory system speed is large, these techniques achieve performance improvements of up to 1700%. While the focus is on the Alpha architecture, many of the covered techniques are readily applicable to other RISC processors and even modern CISC CPUs.
The tricky part in discussing how the same techniques work on other architectures is that we want to do this without igniting a war over which CPU architecture is the “best” or the “fastest”. Such terms are, to a good degree, meaningless, since they can be applied usefully relative to a given problem only. For this reason, performance results are presented as follows: for the Alpha we present both absolute and relative results. The absolute numbers are useful to give a concrete feel for how fast the code is. The relative results (i.e., speed ups) are what tell us how well a given technique works. Where meaningful, we also list the speed up (but not the absolute performance) achieved on a Pentium Pro-based system. Only listing speed up for the Pentium Pro case makes it impossible to tell which system was faster on a given problem while still allowing us to compare the relative benefits. (To avoid any misconception: this arrangement was not chosen because the Alpha performed poorly; the author has been using Alphas for some time now and is generally pleased with the performance level they achieve.)
Since an architecture per se doesn’t perform at all, let us be a bit more specific about the systems used for the measurements:
- Alpha system: The Alpha system was an AlphaStation 600 5/333 (aka Alcor). It has a 333MHz 21164 processor with 4MB of third-level cache and 64MB of main-memory. While a nice (and very expensive) box, it is by no means the latest and greatest of the available Alpha systems. At the time of this writing, much faster and much cheaper 500MHz systems have already been around for a while.
- Pentium Pro system: The x86 system was a Gateway 2000 with a Pentium Pro processor with 32MB of main memory and 256KB of second-level cache. For clarity, this system is referred to as “P6” during the remainder of this section.
Both the Alpha and the P6 systems were running Red Hat 4.0 with kernel version 2.0.18. The compiler used was gcc version 2.7.2. On the Alpha, option -O2 was used (with this version of gcc, using an option setting of -O3 or higher generally results in slower code.). On the P6, options -O6 and -m486 were used.
It is also illustrative to compare gcc to commercial Alpha compilers, such as Digital’s GEM C compiler. The GEM C compiler usually generates somewhat better code but now and then it creates code much faster than gcc’s code (this usually happens on floating-point intensive code). For this reason, some of the measurements also include the results obtained with GEM C. This compiler was invoked as:
cc -migrate -O4 -tune ev5 -std1 -non_shared
It’s not clear which version of the compiler it was—it came with Digital UNIX version 3.2.
Avoiding Integer Division
The Alpha architecture does not provide an integer division instruction. The rationale for this is:
- Such operations are relatively rare.
- Division is fundamentally of an iterative nature, so implementing it in hardware is not all that much faster than a good software implementation. (See Reference 1.)
Nevertheless, there are important routines that depend on integer division. Hash-tables are a good example as computing a hash-table index typically involves dividing by an integer prime constant.
There are basically two ways to avoid integer division. Either the integer division is replaced by a floating-point division or, if the division is by a constant, it is possible to replace the division by a multiplication with a constant, a shift and a correction by one (which isn’t always necessary). Floating-point division may sound like a bad idea, but the Alpha has a very fast floating-point unit, and since a 32-bit integer easily fits into a double without a loss of precision, it works surprisingly well. Replacing a division by a constant with a multiplication by the inverse is certainly faster, although it’s also a bit tricky since care must be taken that the result is always accurate (off-by-one errors are particularly common). Fortunately, for compile-time constants, gcc takes care of this without help.
To illustrate the effect this can have, we measured how long it takes to look up all symbols in the standard C library (libc.so) using the ELF hash-table look-up algorithm (which involves one integer division by a prime constant). With integer division, roughly 1.2 million look ups per second can be performed. Using a double multiplication by the inverse of the divisor instead brings this number up to 1.95 million look ups per second (62% improvement). Using integer multiplication instead gives the best performance of 2.05 million lookups per second (70% improvement). Since the performance difference between the double and the integer multiply-by-inverse version isn’t all that big, it’s usually better to use the floating-point version. This works perfectly well, as long as the operands fit in 52 bits, and avoids having to worry about off-by-one errors.
Keeping the Translation Lookaside Buffer in Mind
Two parts in modern CPUs that are easy to forget are the data and instruction translation lookaside buffers (TLBs). The TLBs hold the most recently accessed page table entries. TLBs are necessary since it would be far too slow to access the page tables on every memory access. Since each TLB entry maps an entire page (8KB with the current Alpha chips), the TLB is usually not the limiting factor to performance. The catch is that when a program does suffer from excessive TLB misses, performance will go down the drain fast. In such a case, the slowdown can easily be big enough that it is worthwhile to switch to a completely different (normally slower) algorithm that has a better TLB behavior. For example, on the Alpha system reading one word from each page in an array of 63 pages (504KB) takes about 15ns per access. But doing the same in an array of 64 pages takes 65ns per access—a slow down of more than a factor of four. Since the second-level cache in that system is 4MB in size, this jump in access time is purely due to the data TLB.
The TLB is not usually a first-order bottleneck but a small experiment did show that a hash table that is 50% full and exceeds the data TLB size is no faster than a more compact search tree that needs two memory accesses per look up (the hash table needs just one memory access, but since it exceeds the TLB size, that one access is slow). In general, the TLB may be the primary bottleneck when large data sets are accessed more or less randomly and sparsely.
Avoiding Memory Accesses
On modern systems, memory accesses are bad and computation is good. In the ideal case, we would like to completely replace memory accesses by computation. This obviously is not always possible; but where it is possible, the payoff can be big.
For example, let us consider the problem of reversing all the bits in each byte in a long integer. A byte is reversed as follows: bit 0 is swapped with bit 7, bit 1 with bit 6 and so on. Since we want to reverse all the bytes in a long, this algorithm is applied once for each byte in the long.
Why would anyone want to do this? As you may know, both the Alpha and the x86 architecture are little-endian, but when IBM designed the VGA graphics adapter, it chose to use a big-endian bit order for the pixels in the graphics memory. That is, bit 7 in a byte corresponds to the left-most pixel and bit 0 to the rightmost. This is backwards since the coordinate value for the left-most pixel is smaller. So, byte reversal is indeed a relatively important operation for VGA X servers.
Listing 1.
u_int byterev_naive (u_int L) {
/* this is for sizeof(u_int)==4 */ return
(((u_int)byte_reversed[(L >> 0) & 0xff] << 0) |
((u_int)byte_reversed[(L >> 8) & 0xff] << 8) |
((u_int)byte_reversed[(L >> 16) & 0xff] << 16) |
((u_int)byte_reversed[(L >> 24) & 0xff] << 24));
}
The traditional way of implementing byte reversal is shown by the code in Listing 1 To conserve space, we show the code to reverse a 4-byte integer only. The 8-byte long case is a straightforward extension of this one. The code assumes that array byte_reversed has been initialized such that byte_reversed[i] is the reversed value of i. With this naive algorithm, each byte reversal involves a table look up.
All listings in this article are available by anonymous download in the file ftp.linuxjournal.com/pub/lj/listings/issue43/2487.tgz.
Listing 2.
u_long byterev_long (u_long L) {
u_long mask = 0x0101010101010101;
return (((L & (mask << 0)) << 7) |
((L >> 7) & (mask << 0)) |
((L & (mask << 1)) << 5) |
((L >> 5) & (mask << 1)) |
((L & (mask << 2)) << 3) |
((L >> 3) & (mask << 2)) |
((L & (mask << 3)) << 1) |
((L >> 1) & (mask << 3)));
}
Since the Alpha is a 64-bit architecture, this means each long reversal involves eight memory accesses. How could we avoid these expensive memory accesses? Well, a simple and arguably more intuitive way to implement byte reversal is to use shifting and masking to swap the bits. The code that does this is shown in Listing 2.
Note that, except for the initialization of mask, this code is completely independent of the width of a long. So, to make this work on a 32-bit machine, all we need to do is initialize mask with 0x01010101 instead.
Now let’s see how the implementations compare. Table 1 gives the results for the Alpha, the Pentium Pro (P6) and a 120MHz Pentium Notebook (P5). In addition to the two implementations shown above, the table also includes a row that shows the performance of the naive implementation when coded in x86 assembly code (implementation byterev_x86). This routine comes straight from the XFree86 v3.2 distribution.
Table 1. Comparison of Byte-Reversal Routines
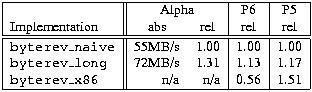
As the table shows, the byte-reversal routine that avoids memory accesses is over 30% faster on the Alpha. Interestingly, on the P6 this routine is also the fastest. The benefit there is less (only 13%), but given that it’s more portable and more intuitive, there is no reason not to use it. What’s stunning is the complete failure of the assembly version on the P6. That routine is only half as fast as the version that avoids memory accesses. This may be due to the assembly routine’s extensive use of byte accesses to CPU registers. For the Pentium notebook, as shown in the P5 column, the assembly-code routine is the fastest version. Don’t be misled by the relative performance numbers; in terms of absolute performance, the P5 is just half as fast as the P6.
To summarize, not only is byterev_long() by far the fastest version on the Alpha, it also appears to be the right solution on a P6.
Lending gcc a Hand
One reason gcc sometimes generates significantly less efficient code than Digital’s GEM compiler is that it does not perform inter-procedural alias analysis. What this means is that gcc’s alias analysis is sometimes unnecessarily conservative. To illustrate the problem, consider the function shown in Listing 3. It is a simple unrolled loop that reverses all the bytes in array src and stores the result in array dst.
Listing 3.
void vecrev_naive (long *src, long *dst,
long size)
{
long i;
for (i = 0; i < size/sizeof(long); i += 4)
{
dst[i + 0] = byterev_long(src[i + 0]);
dst[i + 1] = byterev_long(src[i + 1]);
dst[i + 2] = byterev_long(src[i + 2]);
dst[i + 3] = byterev_long(src[i + 3]);
}
}
The problem with this code is that the C compiler has no way of knowing how the src and dst pointer relate to each other. For all it knows, dst could point to the second element of the array pointed to by src. When this happens, the two pointers refer to overlapping regions of memory and they are said to alias each other. For the compiler, it is important to know whether the two pointers overlap, since that determines the degree of freedom it has in reordering instructions. For example, if the regions overlap, then storing a value to dst[i+0] may affect the value of src[i+1]. Thus, to be on the safe side, the compiler must generate the loads and stores in the above function strictly in the order in which they occur in the source code.
Now, if it is known that the two arrays passed to the function never alias each other, we can lend gcc a hand by explicitly giving it this information. We can do this by first reading all the values from the memory, then doing all the computation and finally storing the results back to memory. Thus, the above code would be transformed into the code shown in Listing 4.
Listing 4.
void vecrev_sep (long *src, long *dst, long size)
{
unsigned long L0, L1, L2, L3;
long i;
for (i = 0; i < size/sizeof(long); i += 4)
{
/* loads: */
L0 = src[i + 0];
L1 = src[i + 1];
L2 = src[i + 2];
L3 = src[i + 3];
/* computation: */
L0 = byterev_long(L0);
L1 = byterev_long(L1);
L2 = byterev_long(L2);
L3 = byterev_long(L3);
/* stores: */
dst[i + 0] = L0;
dst[i + 1] = L1;
dst[i + 2] = L2;
dst[i + 3] = L3;
}
}
Since all of the stores occur at the end, gcc knows immediately that none of the stores can affect any of the preceding loads. This provides it complete freedom in generating the best possible code for the loads and computation (the assumption here is that byterev_long is an in-line function).
On the Alpha and most other architectures with lots of registers (e.g., most RISCs), this kind of code never (or at least very rarely) hurts performance and usually improves performance for gcc. Unfortunately, the same isn’t true for the x86 architecture. The problem there is that only a few registers are available. So, the code that’s better for the RISCs is usually worse for the x86 due to additional stores and loads that are necessary to access the temporaries that end up on the stack. Performance numbers for the two versions are given in Table 2.
Table 2. Performance Values of Byte Reversal Source Code

As the Table 2 shows, merely by separating loads from computation from stores gains 13% with gcc on the Alpha. In contrast, the same code loses 17% on the P6. This illustrates that while most of the techniques in this paper apply to both architectures, there are important differences that sometimes necessitate different coding to achieve the best performance.
Improving the Memory Access Pattern
Now, let’s consider a simple problem: matrix multiplication. While simple, it is typical of a problem that is considered floating-point intensive. In reality, most floating-point intensive problems are also memory intensive. For example, they process large vectors or matrices. Thus, the memory access pattern often plays a crucial role in achieving the best possible performance. The textbook implementation of matrix multiplication looks is shown in Listing 5.
Listing 5.
void matmul0(int dim, float *a, float *b,
float *c)
{
int i, j, k; float dot;
for (i = 0; i < dim; ++i)
for (j = 0; j < dim; ++j)
{
dot = 0.0;i
for (k = 0; k < dim; ++k)
dot += a[i*dim + k] * b[k*dim + j];
c[i*dim + j] = dot;
}
}
Here, the matrix pointed to by a gets multiplied by the matrix pointed to by b and the result is stored in c. The matrix dimension is passed in argument dim. On the Alpha, a 512 by 512 matrix multiply with this routine executes at about thirteen million floating-point operations per second (MFLOPS). This is not too shabby, but let’s see whether we can squeeze more out of the machine. Having learned our lesson in performance optimization, we might try to unroll the inner loop and avoid all multiplications due to indexing. This does indeed result in a faster version: now, matrix multiply executes at about 15 MFLOPS.
gcc‘s optimizer is unable to eliminate the induction variables and, hence, the multiplications due to indexing. gcc 2.72.1 and earlier have a bug in this area that appears when generating code for the Alpha. If the index variables are declared as long instead of int, gcc is able to eliminate the induction variables, as one would expect.
Rather than declaring the problem solved, let’s think about the memory access pattern for a minute. Each element in the result, matrix c, is a dot product of a row in a and a column in b. For example, the element c[0][0] is computed as the dot product of the first row in a and the first column in b. This is illustrated in Figure 1. In our naive matrix-multiply routine, this means that the accesses to a form a nice, dense, linear memory-access pattern. Unfortunately, things do not look quite as good for b. There the memory access pattern is sparse: first, the element at offset 0 is read, then the one at offset dim and so on. Such sparse access patterns are bad for many reasons. Suffice to say it’s easiest to optimize a machine for dense, linear accesses, so it is likely that those accesses will always be the fastest ones. Fortunately, there is a simple trick that avoids the bad access pattern for matrix b: before doing the actual matrix multiply, we can simply transpose matrix b. Then, all memory accesses are dense. Of course, transposing b causes extra work, but since that matrix is accessed dim times, this may well be worth the trouble.
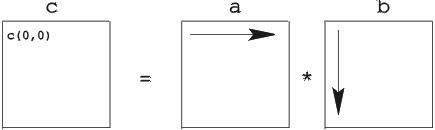
Figure 1: Matrix Multiply
So, let’s change matmul0 into matmul1 by adding a matrix transposition in front of the main loop. The code in Listing 6 assumes that tb is an appropriately sized temporary variable to hold the transposition of b.
Listing 6.
void matmul1(int dim, float *a, float *b,
float *c)
{
int i, j, k; float dot;
/* transpose b: */
for (i = 0; i < dim; ++i)
for (j = 0; j < dim; ++j)
tb[i*dim + j] = b[j*dim + i];
/* ...rest like matmul0, except that b is replaced
by tb... */
}
If you thought 15 MFLOPS is fast, think again: matmul1 executes at a blazing 45 MFLOPS. Next, we’ll add some loop unrolling, etc. For matmul0, this bought us 25%, which isn’t bad at all. If we unroll the loop eight times and do some other straightforward optimizations, we get the code shown in Listing 7. For compactness, it assumes that dim is an integer multiple of eight. Was it worth the trouble? By all means yes: matmul2 clocks at a full 80 MFLOPS. Whether you like this kind of code or not may be a matter of taste, but it is certainly fast.
Listing 7.
void matmul2(int dim, float *a, float *b,
float *c)
{
float dot0, dot1, dot2, dot3, a0, a1, a2,
a3, b0, b1, b2, b3;
float dot4, dot5, dot6, dot7, a4, a5, a6,
a7, b4, b5, b6, b7;
long I, J, i, j, k;
/* ...transpose b into tb like in matmul1...; */
for (I = 0; I < dim*dim; I += dim)
for (j = J = 0; j < dim; ++j, J += dim)
{
dot0 = dot1 = dot2 = dot3 = dot4 = dot5 =
dot6 = dot7 = 0.0;
for (k = 0; k < dim; k += 8)
{
a0 = a[I + k + 0];
b0 = tb[J + k + 0];
a1 = a[I + k + 1];
b1 = tb[J + k + 1];
a2 = a[I + k + 2];
b2 = tb[J + k + 2];
a3 = a[I + k + 3];
b3 = tb[J + k + 3];
a4 = a[I + k + 4];
b4 = tb[J + k + 4];
a5 = a[I + k + 5];
b5 = tb[J + k + 5];
a6 = a[I + k + 6];
b6 = tb[J + k + 6];
a7 = a[I + k + 7];
b7 = tb[J + k + 7];
dot0 += a0 * b0;
dot1 += a1 * b1;
dot2 += a2 * b2;
dot3 += a3 * b3;
dot4 += a4 * b4;
dot5 += a5 * b5;
dot6 += a6 * b6;
dot7 += a7 * b7;
}
c[I + j] = dot0 + dot1 + dot2 + dot3 +
dot4 + dot5 + dot6 + dot7;
}
}
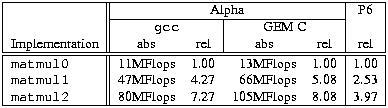
Table 3 presents a summary of the performance results. For comparison, it also includes the results obtained when compiling the same code with Digital’s GEM C compiler and the relative results for the P6. As this table shows, with gcc we achieved a performance improvement by over a factor of seven. More importantly, the optimizations paid off in all three cases. In fact, with Digital’s compiler, the improvement was more than a factor of eight. The performance gap between Digital C and gcc is rather large. For integer code, the gap is usually smaller, but it certainly looks as if gcc needs some work in the floating-point area. Finally, notice that even on the P6 performance increased by almost a factor of four. This is encouraging since unrolling the loop eight times is a tad aggressive for the x86 architecture (because relatively few registers are available). Presumably, the code could be sped up some more, but the point here is that all three cases benefit from memory access optimizations in the same way.
Table 3. Performance Results of Matrix Multiply Routines
Data-parallel Processing: MPEG Core Loop
Multimedia applications are the rage these days. All mainstream CPU architectures (with the notable exception of the PowerPC) have so-called multimedia extensions. The Alpha is ideally suited for such applications since it has been a 64-bit architecture right from the start. In fact, the Alpha multimedia extension is completely trivial; it adds only four new instruction types (vector minimum/maximum, pixel error, pack and unpack). Since some of these instructions can operate on different data types (byte or word, signed or unsigned), the total number of instructions added is 13, which is much smaller than the corresponding number for other architectures. The Alpha got away with so few additions because its original instruction set already contains many of the instructions needed for multimedia applications. For example, there is an instruction that allows eight bytes to be compared in parallel—a seemingly simple instruction that can prove surprisingly powerful in a number of applications.
We illustrate this using mpeg_play, the Berkeley MPEG decoder. (See Reference 2). Since there is not enough space to illustrate all the optimizations that can be applied to this program, we’ll focus on one of the most important operations in the MPEG decoder. This operation involves computing the average of two byte vectors. This is a frequent operation since video often contains images that can be represented as the average of an earlier and a later image. The straightforward way of averaging a byte vector is shown in Listing 8.
Listing 8.
void byte_avg0 (u_long size, u_char *a, u_char *b,
u_char *c)
{
int i;
for (i = 0; i < size; ++i)
c[i] = (a[i] + b[i]) / 2;
}
This loop executes at about 94ns per byte average (iteration) when compiled with gcc. Unrolling this loop twice and reading ahead to the input values needed in the next iteration yields code that is probably close to optimal with this byte-oriented approach. Indeed, with gcc, performance increases to about 60ns per byte average. (Let’s call this unrolled version of the function byte_avg1.)
To get even higher performance, we need to be a bit more aggressive. Considering that the Alpha is a 64-bit architecture, we would like to calculate the average of eight bytes in parallel. Reformulating byte-oriented algorithms in such a data parallel format is often trivial. For byte averaging, it’s not quite as simple. The straightforward implementation requires nine bits of precision, since 255 + 255 = 510. If we pack eight bytes into a 64-bit word, there is no extra ninth bit. How can we get around this? Obviously, we can divide the operands by two before adding them. That way, the sum is at most 127 + 127 = 254 which conveniently fits into eight bits. The catch is that the result may be wrong; if both operands are odd, it will be one too small. Fortunately, it’s easy to correct for this: if bit 0 in both operands is set, a correction by one is necessary. In other words, we can make space for that extra ninth bit by using an additional long register that is used to hold the correction bits. Since all intermediary results now fit into eight bits, the obstacles to a data-parallel implementation of byte averaging have been removed.
Listing 9
#define CAT(v,x) ((u_long)(v)<<8 | (x))
#define VEC(x)
CAT(CAT(CAT(CAT(CAT(CAT(CAT(x,x),x),x),x),x),x),x)
void byte_avg2 (u_long size, u_char *ca,
u_char *cb, u_char *cc)
{
u_long *a = (u_long*) ca;
u_long *b = (u_long*) cb;
u_long *c = (u_long*) cc;
u_long A0 = a[0], B0 = b[0], A1, B1, CC, i,
count = size / sizeof(u_long);
for (i = 1; i < count; )
{
A1 = a[i];
/* read ahead */
B1 = b[i]; ++i;
CC = (A0 & B0) & VEC(0x01);
A0 = (A0 >> 1) & VEC(0x7f);
B0 = (B0 >> 1) & VEC(0x7f);
c[i - 2] = A0 + B0 + CC;
/* read ahead */
A0 = a[i]; B0 = b[i]; ++i;
CC = (A1 & B1) & VEC(0x01);
A1 = (A1 >> 1) & VEC(0x7f);
B1 = (B1 >> 1) & VEC(0x7f);
c[i - 2] = A1 + B1 + CC;
}
}
The resulting code is shown in Listing 9. For simplicity, it assumes that the input vectors are long aligned and have a size that is an integer multiple of the size of a long. Note that macro VEC() takes an eight-bit value and replicates it once for each byte in a long—it’s much more convenient and less error-prone to write VEC(0x01) instead of 0x0101010101010101. Maybe it’s helpful to explain the core of the averaging a bit. Variable CC holds the correction bits, so it’s simply the bitwise AND of vectors A0 and B0, masked with a vector of 0x01. We divide A0 and B0 by two by shifting them to the right by one position and masking the resulting long with a vector of 0x7f. This masking is necessary since otherwise bit 0 of the byte “above” a byte would sneak in and become bit 7 of that byte, causing gross errors. The average is computed by simply adding the vectors A0, B0, and CC. This addition does not cause any overflows since, per byte, the largest possible value is 127 + 127 + 1 = 255.
Despite its look, this code is actually very portable. For a 32-bit architecture, all that needs to change is macro VEC (and even that is necessary only to get rid of compiler warnings). Byte order is not an issue since even though the data is accessed one long at a time, each byte is still processed individually. This data-parallel version of the byte-averaging loop runs at 5.3ns per byte-average—more than an order of magnitude faster than the unrolled loop.
A summary of the three averaging routines is given in Table 4. The relative performance is in terms of throughput (number of byte-averages per second) since that’s both more intuitive and more impressive. Results for the Alpha are presented both for gcc and Digital’s GEM C compiler; as usual, for the P6, gcc was used.
Table 4. Performance of Averaging Routines
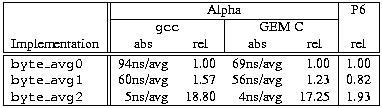
Note that GEM C generates much better code for the stupid version (byte_avg0) but just slightly better code for the clever version (byte_avg2). This is a common theme, at least for integer code: for well-structured code, gcc usually generates code that is on par with the GEM C compiler. The other interesting result is that the read ahead and loop-unrolling hurt on the P6. This means that byte_avg2 probably could be optimized more for the P6 (since it uses read ahead and loop-unrolling, too), but even so the P6 is twice as fast with the data-parallel version. This is impressive since the relative overheads are much higher for a 32-bit chip (the Alpha can amortize all the masking and shifting over eight bytes, whereas a 32-bit architecture has only four bytes).
How does all this affect performance of mpeg_play? This is best illustrated by comparing the original Berkeley version with the one optimized using the techniques described in this section (particularly data-parallel processing and avoiding integer divisions). (See Reference 3.) Comparing MPEG performance is a bit tricky since a large fraction of the time is spent displaying images. This can be factored out by using the option -dither<\!s>none, which has the effect that nothing gets displayed (while the MPEG stream is still decoded as usual). Table 5 shows the result for this mode as well as when using an ordered dither. The ordered dither itself was also optimized using data-parallel processing, which resulted in a version called ordered4. The options used for mpeg_play were -controls<\!s>none<\!s>-framerate<\!s>0<\!s>-dither<\!s>D. The value of D was either none, ordered or ordered4, as indicated in column labeled “Dither” in Table 5. The movie that was used in these measurements was a 320 by 240 pixel-sized computer animation called RedsNightmare.mpg. (See Reference 4.)
Table 5. MPEG Performance Values
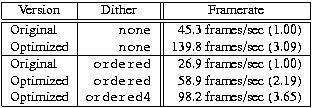
As the table shows, the optimization techniques do indeed result in tremendous performance improvements even at the application level. Of course, few people would enjoy watching a movie at 98 frames per second, but with the optimized code, you can either watch much larger videos in real-time, or you could have CNN on while watching your favorite movie. Who needs picture-in-picture capability when we’ve got real windowing systems?
Conclusions
The Alpha architecture is designed for performance and its implementations do indeed make for very fast systems. Since its chips run at very high clock frequencies, the Alpha usually benefits the most from simple techniques that improve the memory-system behavior of a given program or algorithm. A few of these techniques have been demonstrated in this article and shown to achieve performance improvements anywhere in the range of 10% to 1700%. Fortunately, the same techniques also seem to benefit the other CPU architectures. This is good news since it means that usually one optimized implementation will perform well across a broad range of CPUs.
The biggest hurdle to developing high-performance applications under Linux is the current lack of sophisticated performance analysis tools. The relative lack of such tools is not surprising; while most commercial Unix vendors have tools for their own architecture, few, if any, are multi-platform. To some degree this is inherent in the problem, but there is no question it would not be very difficult to create even better portable performance-analysis tools.
Linux is what makes low-cost Alpha-based Unix workstations a reality. While Digital UNIX currently comes with better compilers, runtime libraries and more tools for the Alpha, the price difference is such that one can easily make up for the performance difference by spending a little more money on a faster machine. Also, development of gcc and better libraries doesn’t stand still. However, since most work is done on a voluntary basis, it does take some time. Even so, Linux is already a highly competitive platform for integer-intensive applications. For floating-point intensive and especially FORTRAN applications, things are not yet so mature. Fortunately, if one cannot afford to wait for a better compiler, there is always the option of purchasing one of the commercial FORTRAN compilers available for Linux/Alpha.
Acknowledgments
The author would like to thank Richard Henderson of Texas A&M University and Erik Troan of Red Hat Software for reviewing this paper on short notice. Their feedback greatly improved its quality. Errors and omissions are the sole responsibility of the author. This article was first given as a speech at Linux Expo 97 on April 5.

 Linux, Linux OS, Free Linux Operating System, Linux India Linux, Linux OS,Free Linux Operating System,Linux India supports Linux users in India, Free Software on Linux OS, Linux India helps to growth Linux OS in India
Linux, Linux OS, Free Linux Operating System, Linux India Linux, Linux OS,Free Linux Operating System,Linux India supports Linux users in India, Free Software on Linux OS, Linux India helps to growth Linux OS in India